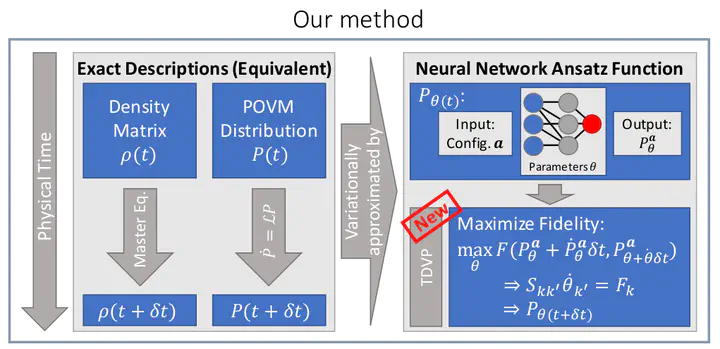
Artificial Neural Networks (ANNs) have proven to be powerful function approximators in many realms of physics. Among many other achievements, they present a competetive approach to the solution of the quantum many-body problem, utilizing state of the art network-designs that represent inherent physical properties of the system under scrutiny, e.g. translational symmetry in convolutional networks. While promising results have been obtained for the time evolution in the case of closed quantum systems in which the ANN serves as a variational wave function, the more general case of the dynamics of open quantum systems has not received as much attention. Here, we encode the density matrix by its corresponding POVM probability distribution which is represented through the parameters of an ANN for which we explicitly construct updates corresponding to dissipative Lindbladian dynamics. This is achieved using a Time Dependent Variational Principle, allowing us to accurately recreate the Lindbladian dynamics on the variational manifold.
Moritz Reh
PhD Student
